1932
0
  1. Home
  2. A-Z Publications
  3. Annual Review of Statistics and Its Application
  4. Volume 8, 2021
  5. Article

Annual Review of Statistics and Its Application

Volume 8, 2021

Compositional Data Analysis

Abstract

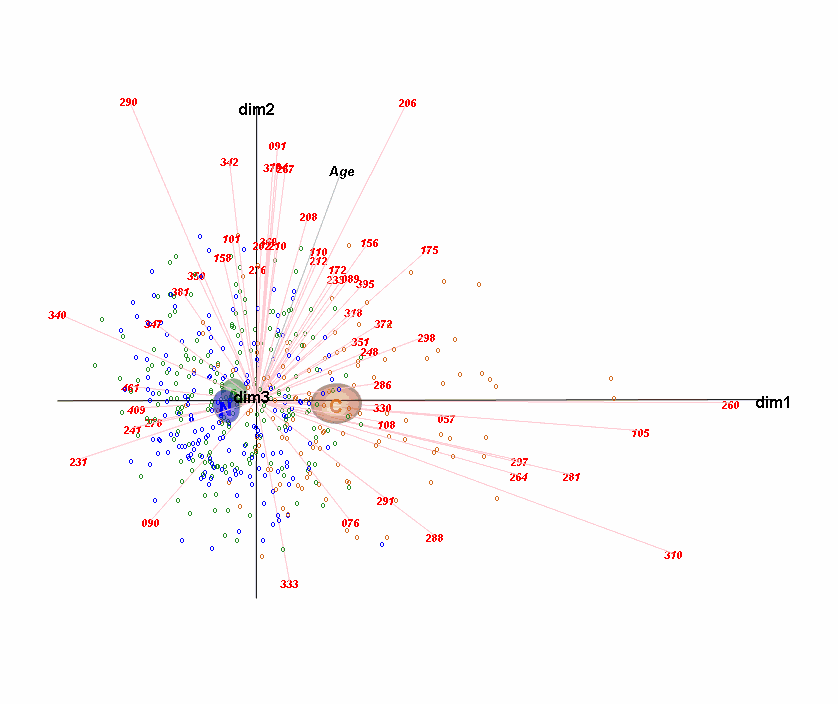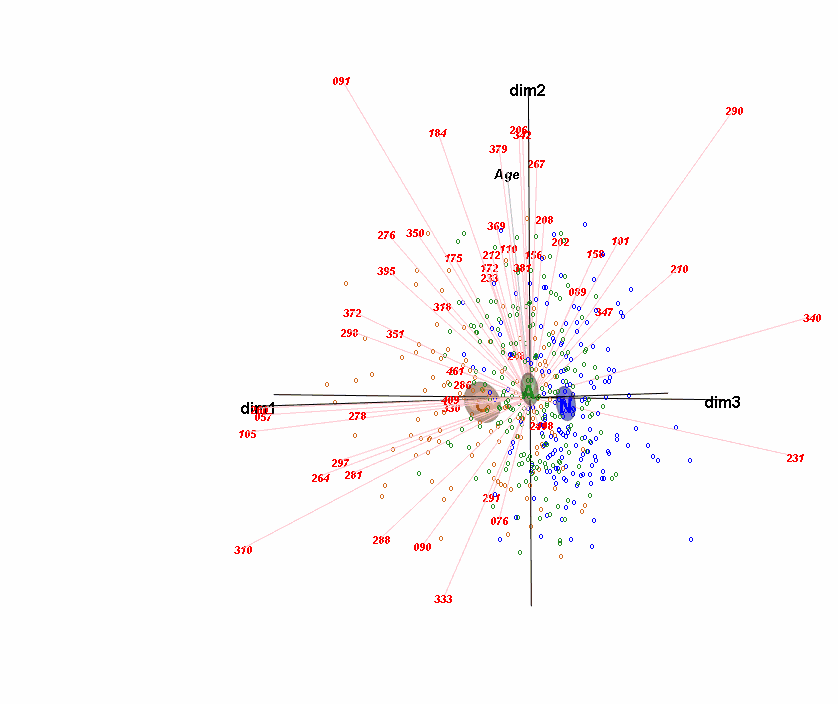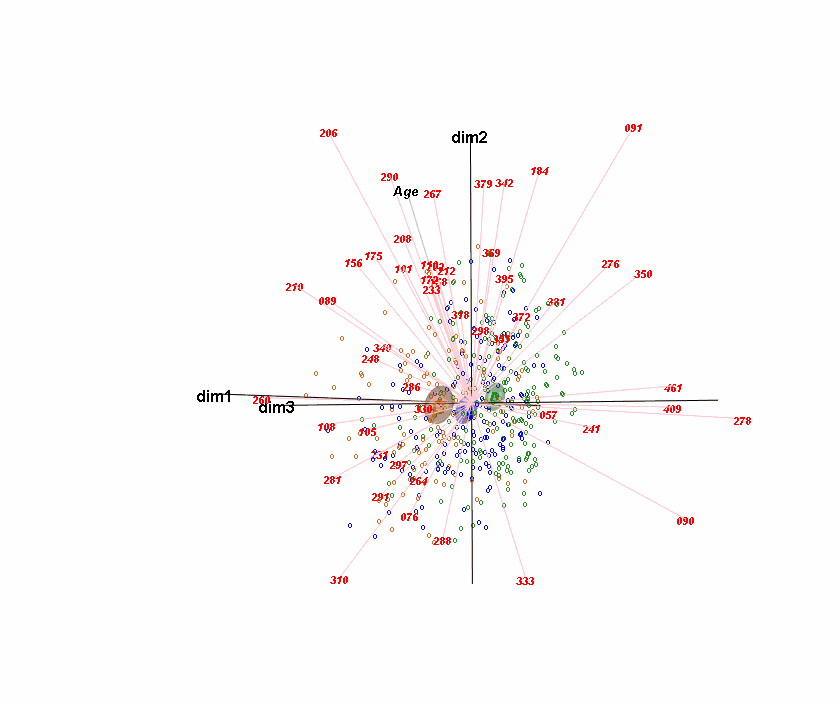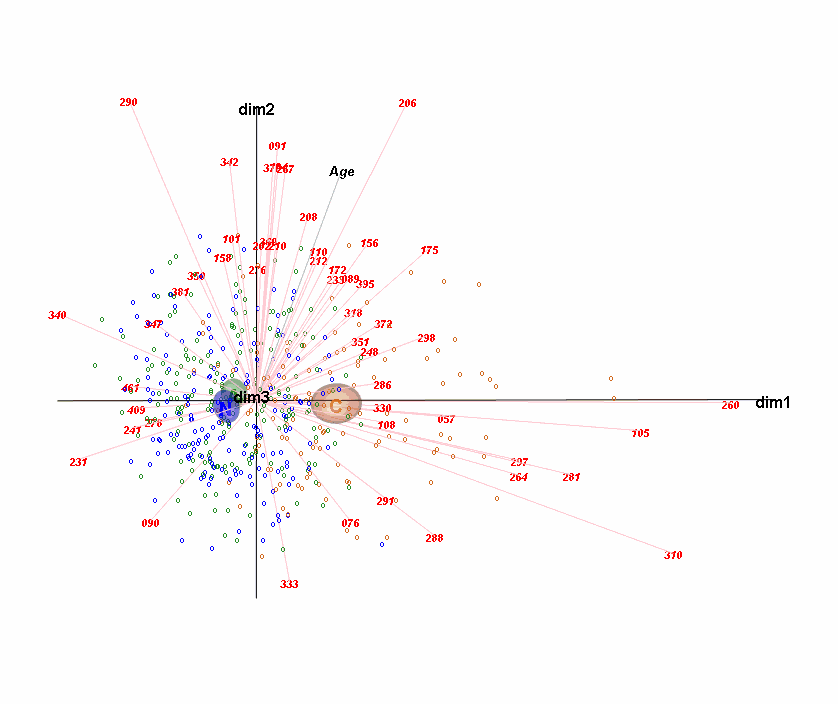
Compositional data are nonnegative data carrying relative, rather than absolute, information—these are often data with a constant-sum constraint on the sample values, for example, proportions or percentages summing to 1% or 100%, respectively. Ratios between components of a composition are important since they are unaffected by the particular set of components chosen. Logarithms of ratios (logratios) are the fundamental transformation in the ratio approach to compositional data analysis—all data thus need to be strictly positive, so that zero values present a major problem. Components that group together based on domain knowledge can be amalgamated (i.e., summed) to create new components, and this can alleviate the problem of data zeros. Once compositional data are transformed to logratios, regular univariate and multivariate statistical analysis can be performed, such as dimension reduction and clustering, as well as modeling. Alternative methodologies that come close to the ideals of the logratio approach are also considered, especially those that avoid the problem of data zeros, which is particularly acute in large bioinformatic data sets.

Keyword(s): amalgamation, coherence, composition, correspondence analysis, count data, logratios, redundancy analysis, regression, subcomposition
Loading

Article metrics loading...

/content/journals/10.1146/annurev-statistics-042720-124436
2021-03-07
2024-04-29
Loading full text...

Full text loading...

/deliver/fulltext/statistics/8/1/annurev-statistics-042720-124436.html?itemId=/content/journals/10.1146/annurev-statistics-042720-124436&mimeType=html&fmt=ahah

Literature Cited

  1. Aitchison J. 1981. A new approach to null correlations of proportions. Math. Geol. 13:175–89
     [Google Scholar]
  2. Aitchison J. 1982. The statistical analysis of compositional data (with discussion). J. R. Stat. Soc. Ser. B 44:139–77
     [Google Scholar]
  3. Aitchison J. 1983. Principal component analysis of compositional data. Biometrika 70:57–65
     [Google Scholar]
  4. Aitchison J. 1986. The Statistical Analysis of Compositional Data London: Chapman and Hall
  5. Aitchison J. 1990. Relative variation diagrams for describing patterns of variability of compositional data. Math. Geol. 22:487–512
     [Google Scholar]
  6. Aitchison J. 1997. The one-hour course in compositional data analysis, or compositional data analysis is simple. Proceedings of IAMG'97, the Third Annual Conference of the International Association for Mathematical Geology V Pawlowsky-Glahn 3–35 Barcelona: CIMNE
     [Google Scholar]
  7. Aitchison J. 2005. A concise guide to compositional data analysis. Proceedings of CoDaWork05 http://ima.udg.edu/Activitats/CoDaWork05/A_concise_guide_to_compositional_data_analysis.pdf
    [Google Scholar]
  8. Aitchison J. 2008. The single principle of compositional data analysis, continuing fallacies, confusions and misunderstandings and some suggested remedies Keynote address presented at CoDaWork08 Girona, Spain: May 27–30. https://core.ac.uk/download/pdf/132548276.pdf
  9. Aitchison J, Bacon-Shone J. 1984. Log contrast models for experiments with mixtures. Biometrika 71:323–30
     [Google Scholar]
  10. Aitchison J, Greenacre M. 2002. Biplots for compositional data. J. R. Stat. Soc. Ser. A 51:375–92
     [Google Scholar]
  11. Aitchison J, Shen SM 1984. Measurement error in compositional data. Math. Geol 16:637–50
     [Google Scholar]
  12. Bacon-Shone J. 2011. A short history of compositional data analysis. Compositional Data Analysis: Theory and Applications V Pawlowsky-Glahn, A Buccianti 3–11 New York: Wiley
     [Google Scholar]
  13. Baxter MJ, Cool HEM, Heyworth MP 1990. Principal component and correspondence analysis of compositional data: some similarities. J. Appl. Stat. 17:229–35
     [Google Scholar]
  14. Baxter N, Ruffin M, Rogers M, Schloss P 2016. Microbiota-based model improves the sensitivity of fecal immunochemical test for detecting colonic lesions. Genom. Med. 8:37
     [Google Scholar]
  15. Benzécri J-P. 1973. Analyse des Données, Tôme 1: L'Analyse des Correspondances Paris: Dunod
     [Google Scholar]
  16. Borg I, Groenen PJF. 2010. Modern Multidimensional Scaling: Theory and Applications New York: Springer. , 2nd. ed.
  17. Coenders G, Pawlowsky-Glahn V. 2020. On interpretations of tests and effect sizes in regression models with a compositional predictor. SORT 20:201–20
     [Google Scholar]
  18. Combettes PL, Müller CL. 2019. Regression models for compositional data: general log-contrast formulations, proximal optimization, and microbiome data applications. arXiv:1903.01050v1 [math.ST]
  19. Egozcue JJ, Pawlowsky-Glahn V. 2005. Groups of parts and their balances in compositional data analysis. Math. Geol. 37:795–828
     [Google Scholar]
  20. Egozcue JJ, Pawlowsky-Glahn V, Mateu-Figueras G, Barceló-Vidal C 2003. Isometric logratio transformations for compositional data analysis. Math. Geol. 35:279–300
     [Google Scholar]
  21. Erb I, Notredame C. 2016. How should we measure proportionality on relative gene expression data. ? Theory Biosci 135:21–36
     [Google Scholar]
  22. Faes C, Molenberghs G, Hens N, Muller A, Goossens H, Coenen S 2011. Analysing the composition of outpatient antibiotic use: a tutorial on compositional data analysis. J. Antimicrob. Chemother. 66:vi89–94
     [Google Scholar]
  23. Filzmoser P, Hron K, Templ M 2018. Applied Compositional Data Analysis Oxford, UK: Oxford Univ. Press
  24. Gittins R. 1985. Canonical Analysis: A Review with Applications in Ecology Berlin: Springer-Verlag
  25. Gloor GB, MacKlaim JM, Pawlowsky-Glahn V, Egozcue JJ 2017. Microbiome datasets are compositional: and this is not optional. Front. Microbiol. 8:2224
     [Google Scholar]
  26. Gloor GB, Reid G. 2016. Compositional analysis: a valid approach to analyze microbiome high-throughput sequencing data. Can. J. Microbiol. 62:692–703
     [Google Scholar]
  27. Gower J, Dijksterhuis GB. 2004. Procrustes Problems New York: Springer
  28. Graeve M, Greenacre M. 2020. The selection and analysis of fatty acid ratios: a new approach for the univariate and multivariate analysis of fatty acid trophic markers in marine organisms. Limnol. Oceanogr. Methods 18:196–210
     [Google Scholar]
  29. Greenacre M. 2009. Power transformations in correspondence analysis. Comput. Stat. Data Anal. 53:3107–16
     [Google Scholar]
  30. Greenacre M. 2010a. Biplots in Practice Bilbao, Spain: BBVA Found https://www.multivariatestatistics.org
  31. Greenacre M. 2010b. Log-ratio analysis is a limiting case of correspondence analysis. Math. Geosci. 42:129–34
     [Google Scholar]
  32. Greenacre M. 2011a. Compositional data and correspondence analysis. Compositional Data Analysis: Theory and Applications V Pawlowsky-Glahn, A Buccianti 104–13 New York: Wiley
     [Google Scholar]
  33. Greenacre M. 2011b. Measuring subcompositional incoherence. Math. Geosci. 43:681–93
     [Google Scholar]
  34. Greenacre M. 2013. Contribution biplots. J. Comput. Graph. Stat. 22:107–22
     [Google Scholar]
  35. Greenacre M. 2016a. Correspondence Analysis in Practice Boca Raton, FL: Chapman and Hall/CRC Press
  36. Greenacre M. 2016b. Data reporting and visualization in ecology. Polar Biol 39:2189–205
     [Google Scholar]
  37. Greenacre M. 2017. `Size' and `shape' in the measurement of multivariate proximity. Methods Ecol. Evol. 8:1415–24
     [Google Scholar]
  38. Greenacre M. 2018. Compositional Data Analysis in Practice Boca Raton: Chapman and Hall/CRC
  39. Greenacre M. 2019. Variable selection in compositional data analysis using pairwise logratios. Math. Geosci. 51:649–82
     [Google Scholar]
  40. Greenacre M. 2020. Amalgamations are valid in compositional data analysis, can be used in agglomerative clustering, and their logratios have an inverse transformation. Appl. Comput. Geosci. 5:100017
     [Google Scholar]
  41. Greenacre M, Grunsky E, Bacon-Shone J 2020. A comparison of amalgamation and isometric logratios in compositional data analysis. Comput. Geosci. In press. https://doi.org/10.1016/j.cageo.2020.104621
    [Crossref] [Google Scholar]
  42. Greenacre M, Lewi PJ. 2009. Distributional equivalence and subcompositional coherence in the analysis of compositional data, contingency tables and ratio-scale measurements. J. Classif. 26:29–54
     [Google Scholar]
  43. Hron K, Filzmoser P, de Caritat P, Fiserova E, Gardlo A 2017. Model-based replacement of rounded zeros in compositional data: classical and robust approaches. Math. Geosci. 49:797–814
     [Google Scholar]
  44. Jackson DA. 1997. Compositional data in community ecology: the paradigm or peril of proportions. ? Ecology 78:928–40
     [Google Scholar]
  45. Krzanowski WJ. 1987. Selection of variables to preserve multivariate data structure, using principal components. J. R. Stat. Soc. Ser. A 36:22–33
     [Google Scholar]
  46. Lewi PJ. 1976. Spectral mapping, a technique for classifying biological activity profiles of chemical compounds. Arz. Forsch. 26:1295–300
     [Google Scholar]
  47. Lewi PJ. 1986. Analysis of biological activity profiles by Spectramap. Eur. J. Med. Chem. 21:155–62
     [Google Scholar]
  48. Lewi PJ. 2005. Spectral mapping, a personal and historical account of an adventure in multivariate data analysis. Chem. Intell. Lab. Syst. 77:215–23
     [Google Scholar]
  49. Li H. 2015. Microbiome, metagenomics and high-dimensional compositional data analysis. Annu. Rev. Stat. Appl. 2:73–94
     [Google Scholar]
  50. Lovell D, Pawlowsky-Glahn V, Egozcue JJ, Marguerat S, Bähler J 2015. Proportionality: a valid alternative to correlation for relative data. PLOS Comput. Biol. 11(3):e1004075
     [Google Scholar]
  51. Martín-Fernández JA, Barceló-Vidal C, Pawlowsky-Glahn V 2003. Dealing with zeros and missing values in compositional data sets using nonparametric imputation. Math. Geol. 35:253–78
     [Google Scholar]
  52. Martín-Fernández JA, Hron K, Templ M, Filzmoser P, Palarea-Albaladejo J 2012. Model-based replacement of rounded zeros in compositional data: classical and robust approaches. Comput. Stat. Data. Anal. 56:2688–704
     [Google Scholar]
  53. Mert C, Filzmoser P, Hron K 2016. Error propagation in compositional data analysis: theoretical and practical considerations. Math. Geosci. 48:941–61
     [Google Scholar]
  54. Mosimann JE. 1962. On the compound multinomial distribution, the multivariate β-distribution, and correlations among proportions. Biometrika 49:65–82
     [Google Scholar]
  55. Müller I, Hron K, Fišerová E, Šmahaj J, Cakirpaloglu P, Vančaková J 2018. Interpretation of compositional regression with application to time budget analysis. Austrian J. Stat. 47:3–19
     [Google Scholar]
  56. Nenadić O, Greenacre M. 2007. Correspondence analysis in R, with two- and three-dimensional graphics: the package. J. Stat. Softw. 20: http://dx.doi.org/10.18637/jss.v020.i03
    [Crossref] [Google Scholar]
  57. Oksanen J, Blanchet FG, Friendly M, Kindt R, Legendre P et al. 2019. vegan: community ecology package. R package version 2.5-6. https://CRAN.R-project.org/package=vegan
    [Google Scholar]
  58. Palarea-Albaladejo J, Martín-Fernández JA. 2015. zCompositions—R package for multivariate imputation of left-censored data under a compositional approach. Chemometr. Intell. Lab. 143:85–96
     [Google Scholar]
  59. Palarea-Albaladejo J, Martín-Fernández JA, Gómez-García J 2007. A parametric approach for dealing with compositional rounded zeros. Math. Geol. 39:625–45
     [Google Scholar]
  60. Pawlowsky-Glahn V, Buccianti A. 2011. Compositional Data Analysis: Theory and Applications New York: Wiley
  61. Pearson K. 1897. Mathematical contributions to the theory of evolution.—On a form of spurious correlation which may arise when indices are used in the measurements of organs. Proc. R. Soc. 60:489–98
     [Google Scholar]
  62. Peres-Neto PR, Jackson DA. 2001. How well do multivariate data sets match? The advantages of a Procrustean superimposition approach over the Mantel test. Oecologia 129:169–78
     [Google Scholar]
  63. Quinn TP, Erb I. 2020. Amalgams: data-driven amalgamation for the reference-free dimensionality reduction of zero-laden compositional data. bioRxiv 968677. https://www.biorxiv.org/content/10.1101/2020.02.27.968677v1
  64. Quinn TP, Erb I, Richardson MF, Crowley TM 2018. Understanding sequencing data as compositions: an outlook and overview. Bioinformatics 34:2870–78
     [Google Scholar]
  65. Quinn TP, Richardson MF, Lovell D, Crowley TM 2017. propr: an R-package for identifying proportionally abundant features using compositional data analysis. Sci. Rep. 7:16252
     [Google Scholar]
  66. book 2020. R: a language and environment for statistical computing. Statistical Software R Found. Stat. Comput Vienna:
     [Google Scholar]
  67. Shi P, Zhang A, Li H 2016. Regression analysis for microbiome compositional data. Ann. Appl. Stat. 10:1019–40
     [Google Scholar]
  68. Søreide JE, Leu E, Berge J, Graeve M, Falk-Petersen S 2010. Timing of blooms, algal food quality and Calanus glacialis reproduction and growth in a changing Arctic. Glob. Change Biol. 16:3154–63
     [Google Scholar]
  69. Stewart C. 2017. An approach to measure distance between compositional diet estimates containing essential zeros. J. Appl. Stat. 44:1137–52
     [Google Scholar]
  70. Templ M, Hron K, Filzmoser P 2011. robCompositions: an R-package for robust statistical analysis of compositional data. Compositional Data Analysis: Theory and Applications V Pawlowsky-Glahn, A Buccianti 341–55 New York: Wiley
     [Google Scholar]
  71. ter Braak C. 1986. Canonical correspondence analysis: a new eigenvector technique for multivariate direct gradient analysis. Ecology 67:1167–79
     [Google Scholar]
  72. Tolosana-Delgado R, van den Boogaart KG 2011. Linear models with compositions in R. Compositional Data Analysis: Theory and Applications V Pawlowsky-Glahn, A Buccianti 356–71 New York: Wiley
     [Google Scholar]
  73. Tsilimigras MCB, Fodor AA. 2016. Compositional data analysis of the microbiome: fundamentals, tools, and challenges. Ann. Epidemiol. 26:330–35
     [Google Scholar]
  74. van den Boogaart KG, Tolosana-Delgado R 2013. Analyzing Compositional Data with R Berlin: Springer-Verlag
  75. van den Wollenberg AL. 1977. Redundancy analysis, an alternative for canonical analysis. Psychometrika 42:207–19
     [Google Scholar]
  76. Zuur AF, Ieno EN, Smith GM 2007. Analysing Ecological Data New York: Springer
/content/journals/10.1146/annurev-statistics-042720-124436
Loading
Compositional Data Analysis
Annual Review of Statistics and Its Application 8, 271 (2021); https://doi.org/10.1146/annurev-statistics-042720-124436
/content/journals/10.1146/annurev-statistics-042720-124436
/content/journals/10.1146/annurev-statistics-042720-124436
Loading

Data & Media loading...

Supplemental Material

Supplementary Data

  • Article Type: Review Article

Most Cited Most Cited RSS feed

This is a required field
Please enter a valid email address
Approval was a Success
Invalid data
An Error Occurred
Approval was partially successful, following selected items could not be processed due to error